Multiscale estimators

structure_factor.multiscale_estimators.multiscale_estimator(point_pattern, estimator, subwindows_list, k_list, mean_poisson, m=None, proba_list=None, verbose=True, **kwargs)[source]

Sample from \(Z\) [HGBLachiezeR22] using a PointPattern and a realization from the r.v. \(M\). See the definition of \(Z\) below.

Parameters

  • point_pattern (PointPattern) – An encapsulation of a realization of a point process, the observation window, and (optionally) the intensity of the point process.

  • estimator (str) – Choice of structure factor’s estimator. The parameters of the chosen estimator must be added as keyword arguments. The available estimators are “scattering_intensity”, “tapered_estimator”, “bartlett_isotropic_estimator”, and “quadrature_estimator_isotropic”. See StructureFactor.

  • subwindows_list (list) – List of increasing cubic or ball-shaped AbstractSpatialWindow, typically, obtained using subwindows_list(). The shape of the windows depends on the choice of the estimator. Each element of point_pattern_list will be restricted to these windows to compute \(Z\).

  • k_list (list) – List of wavevectors (or wavenumbers) where the estimator is to be evaluated. Each element is associated with an element of subwindows_list. Typically, obtained using subwindows_list().

  • mean_poisson (int) – Parameter of the Poisson r.v. \(M\) used to compute \(Z\). To use a different distribution of the r.v. \(M\), set mean_poisson=None and specify m_list and proba_list corresponding to \(M\).

  • m (int, optional) – Realization of the positive integer-valued r.v. \(M\) used when mean_poisson=None. Defaults to None.

  • proba_list (list, optional) – List of \(\mathbb{P}(M \geq j)\) used with m when mean_poisson=None. Should contains at least m elements. Defaults to None.

  • verbose (bool, optional) – If “True” and mean_poisson is not None, print the re-sampled values of \(M\). Defaults to False.

Keyword Arguments

kwargs (dict) – Parameters of the chosen estimator of the structure factor. See StructureFactor.

Returns

The obtained value of \(Z\).

Return type

float

Example

from structure_factor.data import load_data
from structure_factor.multiscale_estimators import subwindows_list, multiscale_estimator


# PointPattern 
point_pattern = load_data.load_ginibre()
window = point_pattern.window

# subwindows and k
l_0 = 40
subwindows_list, k = subwindows_list(window, subwindows_type="BoxWindow", param_0=l_0)

# multiscale_estimator
mean_poisson = 85
z = multiscale_estimator(point_pattern, estimator="scattering_intensity", 
                               k_list=k, subwindows_list=subwindows_list, 
                               mean_poisson=mean_poisson)

z
Definition

Let \(\mathcal{X} \in \mathbb{R}^d\) be a stationary point process of which we consider an increasing sequence of sets \((\mathcal{X} \cap W_m)_{m \geq 1}\), with \((W_m)_m\) centered box (or ball)-shaped windows s.t. \(W_s \subset W_r\) for all \(0< s<r\), and \(W_{\infty} = \mathbb{R}^d\). We define the sequence of r.v. \(Y_m = 1\wedge \widehat{S}_m(\mathbf{k}_m^{\text{min}})\), where \(\widehat{S}_m\) is one of the positive, asymptotically unbiased estimators of the structure factor of \(\mathcal{X}\) applied on the observation \(\mathcal{X} \cap W_m\), and \(\mathbf{k}_m^{\text{min}}\) is the minimum allowed wavevector associated with \(W_m\). Then, \(Z\) is defined by,

\[Z = \sum_{j=1}^{M} \frac{Y_j - Y_{j-1}}{\mathbb{P}(M\geq j)}\]

with \(M\) an \(\mathbb{N}\)-valued random variable such that \(\mathbb{P}(M \geq j)>0\) for all \(j\), and \(Y_{0}=0\) [HGBLachiezeR22], [RG15].

structure_factor.multiscale_estimators.coupled_sum_estimator(y_list, proba_list)[source]

The coupled sum estimator of [RG15].

Parameters

  • y_list (list) – List of \(M\) realizations of the r.v. \(Y\).

  • proba_list (list) – List of \(\mathbb{P}(M \geq j)\) with \(1 \leq j \leq M\).

Returns

Obtained value of the coupled sum estimator.

Return type

float

Example

from structure_factor.multiscale_estimators import coupled_sum_estimator

y_list= [3, 2.5, 1.2433, 0.1]
proba_list = [0.5, 0.4, 0.333, 0.21232]
z = coupled_sum_estimator(y_list, proba_list)
z
Definition

Let \((Y_m)_{m\geq 1}\) be a sequence of \(L^2\) approximations of a r.v. \(Y\) each of which can be generated in finite time, for which \(\mathbb{E}^{1/2}[(Y_m - Y)^2]\) converges to zero as \(m\) goes to infinity. The coupled sum estimator of [RG15] is defined by,

\[Z = \sum_{j=1}^{M} \frac{Y_j - Y_{j-1}}{\mathbb{P}(M\geq j)},\]

with \(M\) an \(\mathbb{N}\)-valued random variable such that \(\mathbb{P}(M \geq j)>0\) for all \(j\), and \(Y_{0}=0\).

structure_factor.multiscale_estimators.subwindows_list(window, subwindows_type='BoxWindow', param_0=None, param_max=None, params=None)[source]

Create a list of cubic (or ball)-shaped subwindows of a father window, with the associated minimum allowed wavevectors (or wavenumbers).

Parameters

  • window (AbstractSpatialWindow) – Father window.

  • subwindows_type (str, optional) – Type of the subwindows to be created. The available types are “BoxWindow” and “BallWindow”. The former for cubic and the latter for ball-shaped subwindows. Defaults to “BoxWindow”.

  • param_0 (float, optional) – Parameter (lengthside/radius) of the first subwindow to be created. If not None, an increasing sequence of subwindows with parameters of unit increments is created. The biggest subwindow has parameter param_max if it’s not None, else, the maximum possible parameter. Defaults to None.

  • param_max (float, optional) – Maximum subwindow parameter (lengthside/radius). Used when param_0 is not None. Defaults to None.

  • params (list, optional) – List of parameters (lengthside/radius) of the output subwindows. For a list of parameters of unit increments, param_0 and param_max can be used instead. Defaults to None.

Returns

Return type

(list, list)

Example

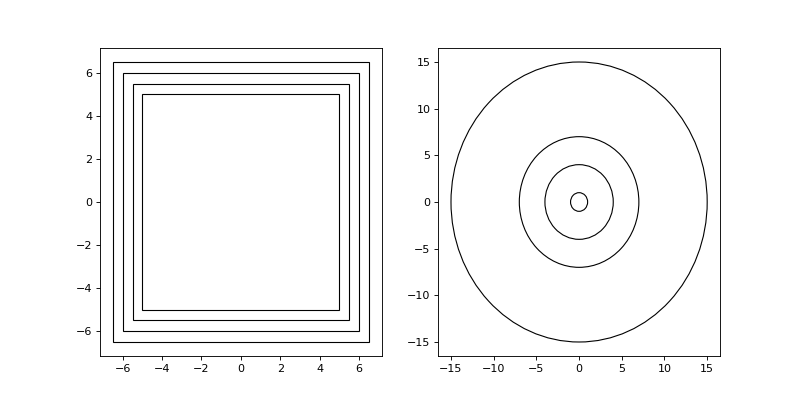
from structure_factor.spatial_windows import BoxWindow
from structure_factor.multiscale_estimators import subwindows_list   

# Example 1: 
L = 30
window = BoxWindow([[-L / 2, L / 2]] * 2)
# subwindows and k
l_0 = 10
subwindows_box, k = subwindows_list(window, subwindows_type="BoxWindow", param_0=l_0)

# Example 2: 
subwindows_params=[1, 4, 7, 15]
subwindows_ball, k_norm = subwindows_list(window, subwindows_type="BallWindow", params=subwindows_params)

import matplotlib.pyplot as plt
fig, axis = plt.subplots(1, 2, figsize=(10,5))
axis[0].plot(0,0)
axis[1].plot(0,0)
for i, j in zip(subwindows_box, subwindows_ball):
    i.plot(axis=axis[0])
    j.plot(axis=axis[1])
plt.show()

(Source code, png, hires.png, pdf)

_images/subwindows1.png

See also

structure_factor.multiscale_estimators.m_threshold(window_min, window_max)[source]

Find the maximum number of integers ranging between the parameters (lengthside/radius) of window_min and the largest subwindow of window_max having the shape of window_min. In particular, it gives the maximum value of the r.v. \(M\) that can be used to compute the multiscale_estimator() given the smallest and biggest subwindow.

Parameters
Returns

Maximum number of integers ranging between the parameters (lengthside/radius) of window_min and the largest subwindow of window_max having the shape of window_min.

Return type

int

Example

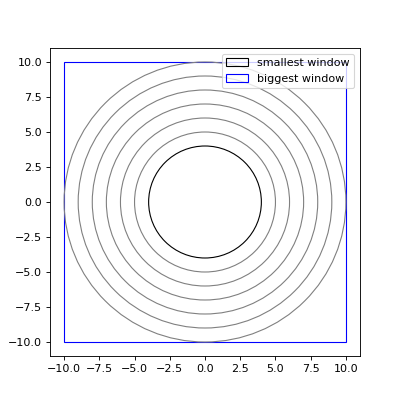
from structure_factor.spatial_windows import BoxWindow, BallWindow
from structure_factor.multiscale_estimators import m_threshold

window_min = BallWindow(center=[0,0], radius=4)
window_max = BoxWindow(bounds=[[-10, 10], [-10, 10]])
m_thresh = m_threshold(window_min, window_max)

import matplotlib.pyplot as plt
fig, axis = plt.subplots( figsize=(5,5))
axis.plot(0,0)
window_min.plot(axis=axis, color="k", label="smallest window")
window_max.plot(axis=axis, color="b", label="biggest window")
for j in range(1, m_thresh+1):
    w = BallWindow(center=[0,0], radius=4+j)
    w.plot(axis=axis, color="grey")
axis.legend()
plt.show()

(Source code, png, hires.png, pdf)

_images/m_threshold.png

See also