Spatial windows

Collection of classes representing observation windows (box, ball, etc).

BallWindow: Ball window object.
BoxWindow: Box window object.

Note

Typical usage

PointPattern has a window argument/attribute.

class structure_factor.spatial_windows.AbstractSpatialWindow[source]

Bases: object

Encapsulate the notion of spatial window in \(\mathbb{R}^d\).

abstract property dimension: Return the ambient dimension of the corresponding window.

abstract property volume: Compute the volume of the corresponding window.

indicator_function(points)[source]

Return the indicator function of the corresponding window evaluated at each of the \(n\) points.

Parameters

points (numpy.ndarray) – Vector of size \(d\) or array of size \(n \times d\) containing the point(s) to be tested.

Returns

If \(n=1\), bool.
If \(n>1\), \(n\) dimensional boolean array.

Return type

bool or numpy.ndarray

abstract rand(n=1, seed=None)[source]

Generate n points uniformly at random in the corresponding spatial window.

Parameters

n (int, optional) – Number of points. Defaults to 1.
seed (int or np.random.Generator, optional) – Defaults to None.

Returns

If \(n=1\), \(d\) dimensional vector.
If \(n>1\), \(n \times d\) array containing the points.

Return type

numpy.ndarray

class structure_factor.spatial_windows.BallWindow(center, radius=1.0)[source]

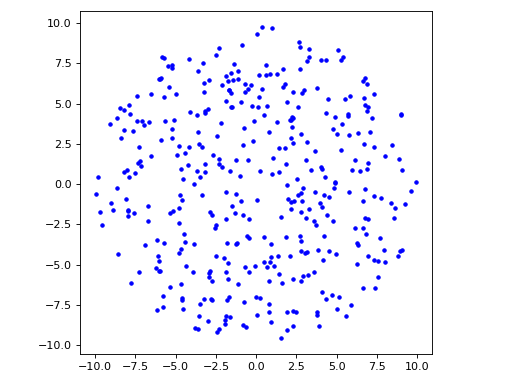
Bases: structure_factor.spatial_windows.AbstractSpatialWindow

Create a \(d\) dimensional ball window \(B(c, r)\), where \(c \in \mathbb{R}^d\) and \(r>0\).

Example

import matplotlib.pyplot as plt

from structure_factor.spatial_windows import BallWindow

window = BallWindow(radius=10, center=[0, 0])
points = window.rand(n=400)

fig, ax = plt.subplots()
ax.plot(points[:, 0], points[:, 1], "b.")
ax.set_aspect("equal", "box")
plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)

See also

__init__(center, radius=1.0)[source]

Initialize a \(d\) dimensional ball window \(B(c, r)\) from the prescribed center and radius.

Parameters

center (numpy.ndarray) – Center \(c\) of the ball.
radius (float, optional) – Radius \(r > 0\) of the ball. Defaults to 1.0.

property dimension: Return the ambient dimension of the corresponding window.

property volume: Compute the volume of the corresponding window.

indicator_function(points)[source]

Return the indicator function of the corresponding window evaluated at each of the \(n\) points.

Parameters

points (numpy.ndarray) – Vector of size \(d\) or array of size \(n \times d\) containing the point(s) to be tested.

Returns

If \(n=1\), bool.
If \(n>1\), \(n\) dimensional boolean array.

Return type

bool or numpy.ndarray

rand(n=1, seed=None)[source]

Generate n points uniformly at random in the corresponding spatial window.

Parameters

n (int, optional) – Number of points. Defaults to 1.
seed (int or np.random.Generator, optional) – Defaults to None.

Returns

If \(n=1\), \(d\) dimensional vector.
If \(n>1\), \(n \times d\) array containing the points.

Return type

numpy.ndarray

to_spatstat_owin(**params)[source]

Convert the object to a spatstat.geom.disc R object of type disc, which is a subtype of owin.

Parameters: params (dict) – Optional keyword arguments passed to spatstat.geom.disc.
Returns: R object.
Return type: spatstat.geom.disc

See also

https://rdocumentation.org/packages/spatstat.geom/versions/2.2-0/topics/disc

plot(axis=None, **kwargs)[source]

Display the window on matplotlib axis.

Parameters: axis (plt.Axes, optional) – Support axis of the plot. Defaults to None.
Keyword Arguments: kwargs (dict) – Keyword arguments of matplotlib.patches.Circle with default fill=False.
Returns: Plot axis.
Return type: plt.Axes

class structure_factor.spatial_windows.UnitBallWindow(center)[source]

Bases: structure_factor.spatial_windows.BallWindow

Create a d-dimensional unit ball window \(B(c, r=1)\), where \(c \in \mathbb{R}^d\).

Note

UnitBallWindow(center) = BallWindow(center, radius=1.0)

__init__(center)[source]

Initialize a \(d\) dimensional unit ball window \(B(c, r=1)\) from the prescribed center.

Parameters: center (numpy.ndarray, optional) – Center \(c\) of the ball.

property dimension: Return the ambient dimension of the corresponding window.

indicator_function(points)

Return the indicator function of the corresponding window evaluated at each of the \(n\) points.

Parameters

points (numpy.ndarray) – Vector of size \(d\) or array of size \(n \times d\) containing the point(s) to be tested.

Returns

If \(n=1\), bool.
If \(n>1\), \(n\) dimensional boolean array.

Return type

bool or numpy.ndarray

plot(axis=None, **kwargs)

Display the window on matplotlib axis.

Parameters: axis (plt.Axes, optional) – Support axis of the plot. Defaults to None.
Keyword Arguments: kwargs (dict) – Keyword arguments of matplotlib.patches.Circle with default fill=False.
Returns: Plot axis.
Return type: plt.Axes

rand(n=1, seed=None)

Generate n points uniformly at random in the corresponding spatial window.

Parameters

n (int, optional) – Number of points. Defaults to 1.
seed (int or np.random.Generator, optional) – Defaults to None.

Returns

If \(n=1\), \(d\) dimensional vector.
If \(n>1\), \(n \times d\) array containing the points.

Return type

numpy.ndarray

to_spatstat_owin(**params)

Convert the object to a spatstat.geom.disc R object of type disc, which is a subtype of owin.

Parameters: params (dict) – Optional keyword arguments passed to spatstat.geom.disc.
Returns: R object.
Return type: spatstat.geom.disc

See also

https://rdocumentation.org/packages/spatstat.geom/versions/2.2-0/topics/disc

property volume: Compute the volume of the corresponding window.

class structure_factor.spatial_windows.BoxWindow(bounds)[source]

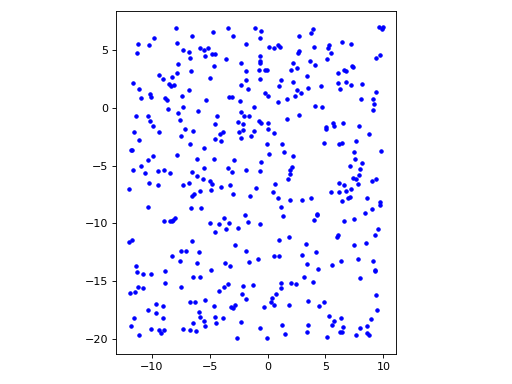
Bases: structure_factor.spatial_windows.AbstractSpatialWindow

Create a \(d\) dimensional box window \(\prod_{i=1}^{d} [a_i, b_i]\).

Example

import matplotlib.pyplot as plt

from structure_factor.spatial_windows import BoxWindow

window = BoxWindow(bounds=[[-12, 10], [-20, 7]])
points = window.rand(n=400)

fig, ax = plt.subplots()
ax.plot(points[:, 0], points[:, 1], "b.")
ax.set_aspect("equal", "box")
plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)

See also

__init__(bounds)[source]

Initialize \(d\) dimensional unit box window the prescibed bounds[i, :] \(=[a_i, b_i]\).

Parameters: bounds (numpy.ndarray) – \(d \times 2\) array describing the bounds of the box.

property bounds

Return the bounds decribing the BoxWindow.

bounds[i, :] \(=[a_i, b_i]\).

property dimension: Return the ambient dimension of the corresponding window.

property volume: Compute the volume of the corresponding window.

indicator_function(points)[source]

Return the indicator function of the corresponding window evaluated at each of the \(n\) points.

Parameters

points (numpy.ndarray) – Vector of size \(d\) or array of size \(n \times d\) containing the point(s) to be tested.

Returns

If \(n=1\), bool.
If \(n>1\), \(n\) dimensional boolean array.

Return type

bool or numpy.ndarray

rand(n=1, seed=None)[source]

Generate n points uniformly at random in the corresponding spatial window.

Parameters

n (int, optional) – Number of points. Defaults to 1.
seed (int or np.random.Generator, optional) – Defaults to None.

Returns

If \(n=1\), \(d\) dimensional vector.
If \(n>1\), \(n \times d\) array containing the points.

Return type

numpy.ndarray

to_spatstat_owin(**params)[source]

Convert the object to a spatstat.geom.owin R object of type owin.

Parameters: params (dict) – Optional keyword arguments passed to spatstat.geom.owin.
Returns: R object.
Return type: spatstat.geom.owin

See also

https://rdocumentation.org/packages/spatstat.geom/versions/2.2-0/topics/owin

plot(axis=None, **kwargs)[source]

Display the window on matplotlib axis.

Parameters: axis (plt.Axes, optional) – Support axis of the plot. Defaults to None.
Keyword Arguments: kwargs (dict) – Keyword arguments of matplotlib.patches.Rectangle with default fill=False.
Returns: Plot axis.
Return type: plt.Axes

class structure_factor.spatial_windows.UnitBoxWindow(center)[source]

Bases: structure_factor.spatial_windows.BoxWindow

Create a \(d\) dimensional unit box window \(\prod_{i=1}^{d} [c_i - \frac{1}{2}, c_i + \frac{1}{2}]\) where \(c \in \mathbb{R}^d\).

__init__(center)[source]

Initialize a \(d\) dimensional unit box window \(\prod_{i=1}^{d} [c_i - \frac{1}{2}, c_i + \frac{1}{2}]\), i.e., a box window with length equal to 1 and prescribed center, such that \(c_i=\) center[i].

Parameters: center (numpy.ndarray) – Center \(c\) of the box.

property bounds

Return the bounds decribing the BoxWindow.

bounds[i, :] \(=[a_i, b_i]\).

property dimension: Return the ambient dimension of the corresponding window.

indicator_function(points)

Return the indicator function of the corresponding window evaluated at each of the \(n\) points.

Parameters

points (numpy.ndarray) – Vector of size \(d\) or array of size \(n \times d\) containing the point(s) to be tested.

Returns

If \(n=1\), bool.
If \(n>1\), \(n\) dimensional boolean array.

Return type

bool or numpy.ndarray

plot(axis=None, **kwargs)

Display the window on matplotlib axis.

Parameters: axis (plt.Axes, optional) – Support axis of the plot. Defaults to None.
Keyword Arguments: kwargs (dict) – Keyword arguments of matplotlib.patches.Rectangle with default fill=False.
Returns: Plot axis.
Return type: plt.Axes

rand(n=1, seed=None)

Generate n points uniformly at random in the corresponding spatial window.

Parameters

n (int, optional) – Number of points. Defaults to 1.
seed (int or np.random.Generator, optional) – Defaults to None.

Returns

If \(n=1\), \(d\) dimensional vector.
If \(n>1\), \(n \times d\) array containing the points.

Return type

numpy.ndarray

to_spatstat_owin(**params)

Convert the object to a spatstat.geom.owin R object of type owin.

Parameters: params (dict) – Optional keyword arguments passed to spatstat.geom.owin.
Returns: R object.
Return type: spatstat.geom.owin

See also

https://rdocumentation.org/packages/spatstat.geom/versions/2.2-0/topics/owin

property volume: Compute the volume of the corresponding window.

structure_factor.spatial_windows.check_cubic_window(window)[source]

Check whether window is cubic.

Parameters: window (BoxWindow) – Window to be checked.

Example

from structure_factor.spatial_windows import BoxWindow, check_cubic_window

# Example 1:
window = BoxWindow(bounds=[[-1, 5], [-1, 2]])
check_cubic_window(window)

# Example 2:
window = BoxWindow(bounds=[[-1, 2], [-1, 2], [-1, 2]])
check_cubic_window(window)

structure_factor.spatial_windows.check_centered_window(window)[source]

Check whether window is centered at the origin.

Parameters: window (AbstractSpatialWindow) – Window to be checked.

Example

from structure_factor.spatial_windows import (
    BoxWindow,
    BallWindow,
    check_centered_window,
)

# Example 1:
window = BoxWindow(bounds=[[-1, 5], [-1, 2]])
check_centered_window(window)

# Example 2:
window = BallWindow(center=[0, 0], radius=5)
check_centered_window(window)

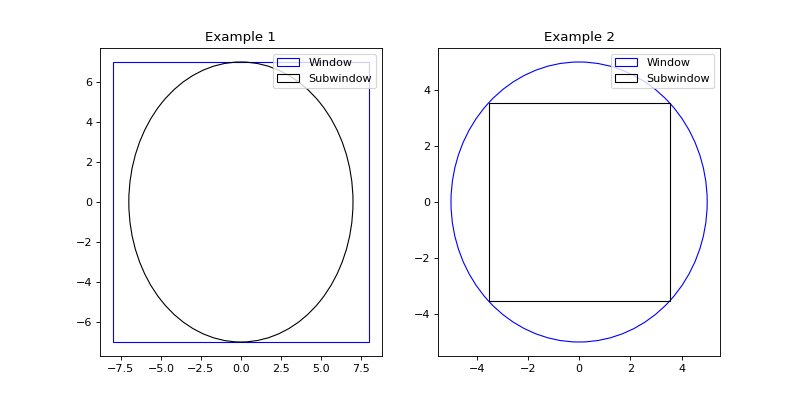
structure_factor.spatial_windows.subwindow_parameter_max(window, subwindow_type='BoxWindow')[source]

Return the parameter i.e., lengthside (resp. radius) of the largest cubic (resp. ball) subwindow of window.

Parameters

window (AbstractSpatialWindow) – BoxWindow or BallWindow centered at the origin.
subwindow_type (str, optional) – Type of the subwindow (“BoxWindow” or “BallWindow”). Defaults to “BoxWindow”.

Returns

Parameter of the largest subwindow of window.

Return type

float

Example

from structure_factor.spatial_windows import (
    BoxWindow,
    BallWindow,
    subwindow_parameter_max,
)

# Example 1:
window1 = BoxWindow([[-8, 8], [-7, 7]])
r = subwindow_parameter_max(window=window1, subwindow_type="BallWindow")
subwindow1 = BallWindow(center=[0,0], radius=r)
# Example 2:
window2 = BallWindow(center=[0, 0], radius=5)
l = subwindow_parameter_max(window=window2)
subwindow2 = BoxWindow([[-l/2,l/2]]*2)

import matplotlib.pyplot as plt
fig, axis = plt.subplots(1, 2, figsize=(10,5))
axis[0].plot(0,0)
window1.plot(axis=axis[0], color="b", label="Window")
subwindow1.plot(axis=axis[0], color="k", label="Subwindow")
axis[0].legend()
axis[0].title.set_text("Example 1")

axis[1].plot(0,0)
window2.plot(axis=axis[1], color="b", label="Window")
subwindow2.plot(axis=axis[1], color="k", label="Subwindow")
axis[1].legend()
axis[1].title.set_text("Example 2")

plt.show()

(Source code, png, hires.png, pdf)