Point processes

Collection of point processes at related properties, e.g., intensity, pair correlation function, structure factor.

class structure_factor.point_processes.HomogeneousPoissonPointProcess(intensity=1.0)[source]

Bases: object

Homogeneous Poisson point process.

__init__(intensity=1.0)[source]

Create a homogeneous Poisson point process with prescribed (positive) intensity parameter.

Parameters

intensity (float, optional) – intensity of the homogeneous Poisson point process. Defaults to 1.0.

property intensity

Return the intensity \(\rho_1(r) = \rho\) of the homogeneous Poisson point process.

Returns

Constant intensity.

Return type

float

static pair_correlation_function(r=None)[source]

Evaluate the pair correlation function \(g(r)=1\) of the homogeneous Poisson process.

Parameters

r (numpy.ndarray) – Array of size \(n \times d\), where \(d\) is the ambient dimension and \(n\) the number of points where the pair correlation function is evaluated. Since the homogeneous Poisson process is isotropic, a vector of size \(n\) corresponding to the norm of the \(n\) points can also be passed. Defaults to None.

Returns

1.0 if r=None, otherwise a vector of size \(n\) with entries equal to 1.0.

Return type

float or numpy.ndarray

static structure_factor(k=None)[source]

Evaluate the structure factor \(S(k)=1\) of the homogeneous Poisson process.

Parameters

k (numpy.ndarray) – Array of size \(n \times d\), where \(d\) is the ambient dimension and \(n\) the number of points where the structure factor is evaluated. Since the homogeneous Poisson process is isotropic, a vector of size \(n\) corresponding to the norm of the \(n\) points can also be passed. Defaults to None.

Returns

1.0 if k=None, otherwise a vector of size \(n\) with entries equal to 1.0.

Return type

float or numpy.ndarray

generate_sample(window, seed=None)[source]

Generate an exact sample of the point process restricted to the \(d\) dimensional window.

Parameters

window (AbstractSpatialWindow) – \(d\)-dimensional observation window where the points will be generated.

Returns

Array of size \(n \times d\), where \(n\) is the number of points forming the sample.

Return type

numpy.ndarray

Example

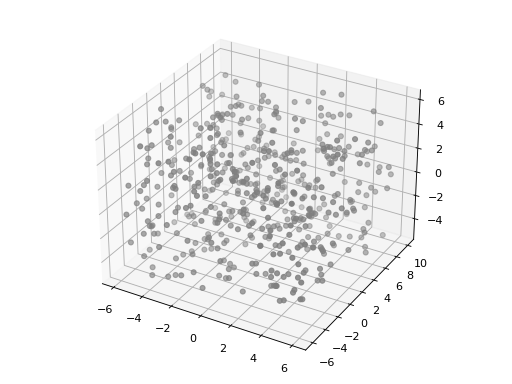
import matplotlib.pyplot as plt

from structure_factor.point_processes import HomogeneousPoissonPointProcess
from structure_factor.spatial_windows import BoxWindow

point_process = HomogeneousPoissonPointProcess(intensity=0.25)

window = BoxWindow([[-6, 6], [-6, 10], [-5, 6]])
points = point_process.generate_sample(window)

ax = plt.axes(projection="3d")
ax.scatter3D(points[:, 0], points[:, 1], points[:, 2], c="grey")

plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)

code/point_processes/poisson_sample.py

See also

generate_point_pattern(window, seed=None)[source]

Generate a PointPattern of the point process.

Parameters

  • window (AbstractSpatialWindow) – Observation window.

  • seed (int, optional) – Seed to initialize the points generator. Defaults to None.

Returns

Object of type PointPattern containing a realization of the point process, the observation window, and (optionally) the intensity of the point process (see PointPattern).

Return type

PointPattern

Example

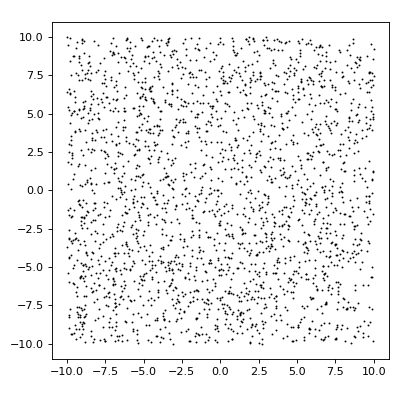
import matplotlib.pyplot as plt

from structure_factor.point_processes import HomogeneousPoissonPointProcess
from structure_factor.spatial_windows import BoxWindow

point_process = HomogeneousPoissonPointProcess(intensity=6)

window = BoxWindow(bounds=[[-10, 10], [-10, 10]])
point_pattern = point_process.generate_point_pattern(window=window)

ax = point_pattern.plot()
ax.set_aspect("equal", "box")
plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)

code/point_processes/poisson_pp.py

See also

class structure_factor.point_processes.ThomasPointProcess(kappa, mu, sigma)[source]

Bases: object

Homogeneous Thomas point process with Gaussian clusters.

__init__(kappa, mu, sigma)[source]

Create a homogeneous Thomas point process.

Parameters

  • kappa (float) – Mean number of clusters per unit volume. Intensity of the parent Poisson point process.

  • mu (float) – Mean number of points per clusters. Mean of the child Gaussian distribution.

  • sigma (float) – Standard deviation of the child Gaussian distribution.

property intensity

Return the intensity \(\rho_1(r) = \kappa \mu\) of the Thomas point process.

Returns

Constant intensity.

Return type

float

pair_correlation_function(r_norm, d=2)[source]

Evaluate the pair correlation function of the Thomas point process.

\[g(r) = 1 + \kappa (4 \pi \sigma^2)^{d / 2} \exp(-\frac{1}{4\sigma^2} \|r\|^2)\]
Parameters

  • r_norm (numpy.ndarray) – Vector of size \(n\) corresponding to the norm of the \(n\) points where the pair correlation function is evaluated.

  • d (int, optional) – Ambient dimension. Defaults to 2.

Returns

Vector of size \(n\) containing the evaluation of the pair correlation function.

Return type

numpy.ndarray

structure_factor(k_norm)[source]

Evaluate the structure factor of the Thomas point process.

\[S(k) = 1 + \mu \exp(- \sigma^2 * \|k\|^2).\]
Parameters

k_norm (numpy.ndarray) – Vector of size \(n\) corresponding to the norm of the \(n\) points where the structure factor is evaluated.

Returns

Vector of size \(n\) containing the evaluation of the structure factor.

Return type

numpy.ndarray

generate_sample(window, seed=None)[source]

Generate an exact sample from the corresponding ThomasPointProcess restricted to the \(d\) dimensional window.

Parameters

window (AbstractSpatialWindow) – \(d\)-dimensional observation window where the points will be generated.

Returns

Array of size \(n \times d\), where \(n\) is the number of points forming the sample.

Return type

numpy.ndarray

Example

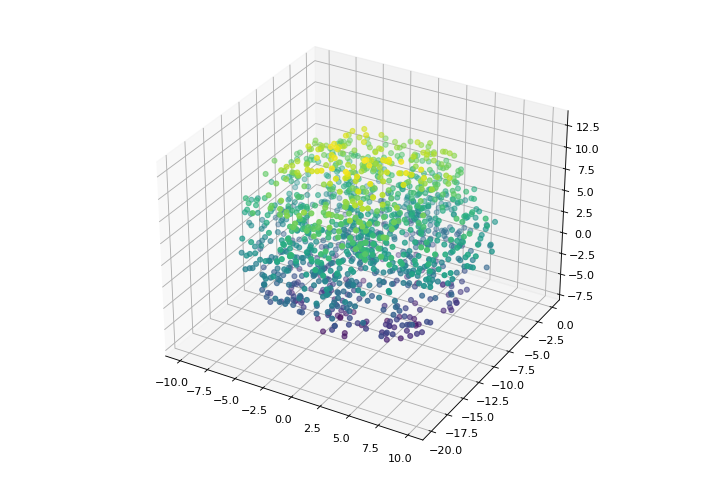
import matplotlib.pyplot as plt
import numpy as np

from structure_factor.point_processes import ThomasPointProcess
from structure_factor.spatial_windows import BallWindow

point_process = ThomasPointProcess(kappa=1 / (5 * np.pi), mu=5, sigma=1)

window = BallWindow(center=[0, -10, 3], radius=10)
points = point_process.generate_sample(window=window)

fig = plt.figure(figsize=(9, 6))
ax = plt.axes(projection="3d")
ax.scatter3D(points[:, 0], points[:, 1], points[:, 2], c=points[:, 2])

plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)

code/point_processes/thomas_sample.py

See also

generate_point_pattern(window, seed=None)[source]

Generate a PointPattern of the point process.

Parameters

  • window (AbstractSpatialWindow) – Observation window.

  • seed (int, optional) – Seed to initialize the points generator. Defaults to None.

Returns

Object of type PointPattern containing a realization of the point process, the observation window, and (optionally) the intensity of the point process (see PointPattern).

Return type

PointPattern

Example

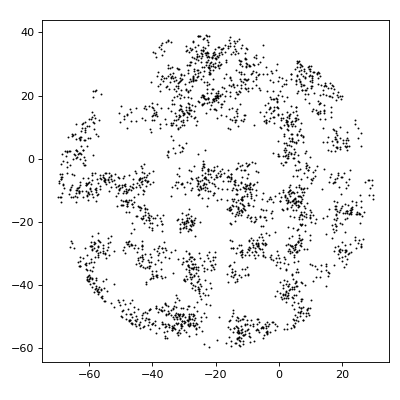
import matplotlib.pyplot as plt
import numpy as np

from structure_factor.point_processes import ThomasPointProcess
from structure_factor.spatial_windows import BallWindow

point_process = ThomasPointProcess(kappa=1 / (20 * np.pi), mu=20, sigma=2)

window = BallWindow(center=[-20, -10], radius=50)
point_pattern = point_process.generate_point_pattern(window=window)

ax = point_pattern.plot()
ax.set_aspect("equal", "box")
plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)

code/point_processes/thomas_pp.py

See also

class structure_factor.point_processes.GinibrePointProcess[source]

Bases: object

Ginibre point process corresponds to the complex eigenvalues of a standard complex Gaussian matrix.

__init__()[source]
property intensity

Return the intensity \(\rho_1(r) = \frac{1}{\pi}\) of the Ginibre point process.

Returns

Constant intensity.

Return type

float

static pair_correlation_function(r_norm)[source]

Evaluate the pair correlation function of the Ginibre point process.

\[g(r) = 1 - \exp(- \|r\|^2)\]
Parameters

r_norm (numpy.ndarray) – Vector of size \(n\) corresponding to the norm of the \(n\) points where the pair correlation function is evaluated.

Returns

Vector of size \(n\) containing the evaluation of the pair correlation function.

Return type

numpy.ndarray

static structure_factor(k_norm)[source]

Evaluate the structure factor of the Ginibre point process.

\[S(k) = 1 - \exp(- \frac{1}{4} \|k\|^2).\]
Parameters

k_norm (numpy.ndarray) – Vector of size \(n\) corresponding to the norm of the \(n\) points where the structure factor is evaluated.

Returns

Vector of size \(n\) containing the evaluation of the structure factor.

Return type

numpy.ndarray

generate_sample(window, n=None, seed=None)[source]

Generate a sample of the Ginibre point process made of n points, inside the observation window.

This is done by computing the eigenvalues of a random matrix \(G\) of size \(n \times n\), filled with i.i.d. standard complex Gaussian variables, i.e.,

\[G_{ij} = \frac{1}{\sqrt{2}} (X_{ij} + \mathbf{i} Y_{ij}).\]
Parameters

  • window (BallWindow) – \(2\)-dimensional centered ball window where the points will be generated.

  • n (int, optional) – Number of points of the output sample. If n is None (default), it is set to the integer part of \(\rho |W| = \frac{1}{\pi} |W|\). Defaults to None.

Returns

Array of size \(n \times 2\), representing the \(n\) points forming the sample.

Return type

numpy.ndarray

Example

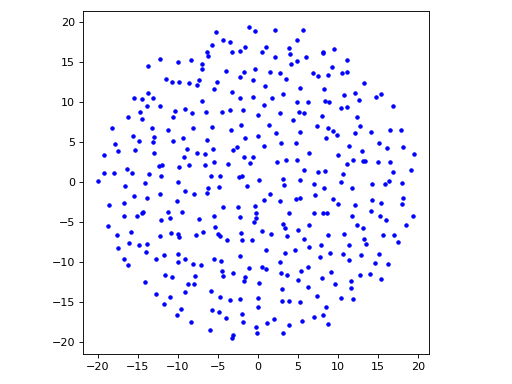
import matplotlib.pyplot as plt

from structure_factor.point_processes import GinibrePointProcess
from structure_factor.spatial_windows import BallWindow

point_process = GinibrePointProcess()

window = BallWindow(center=[0, 0], radius=20)
points = point_process.generate_sample(window=window)

fig, ax = plt.subplots()
ax.plot(points[:, 0], points[:, 1], "b.")
ax.set_aspect("equal", "box")
plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)

code/point_processes/ginibre_sample.py

See also

generate_point_pattern(window, n=None, seed=None)[source]

Generate a \(2\)-dimensional PointPattern of the point process, with a centered BallWindow.

Parameters

  • window (AbstractSpatialWindow) – \(2\)-dimensional observation centered BallWindow.

  • n (int, optional) – Number of points of the output sample. If n is None (default), it is set to the integer part of \(\rho |W| = \frac{1}{\pi} |W|\). Defaults to None.

  • seed (int, optional) – Seed to initialize the points generator. Defaults to None.

Returns

Object of type PointPattern containing a realization of the point process, the observation window, and (optionally) the intensity of the point process (see PointPattern).

Return type

PointPattern

Example

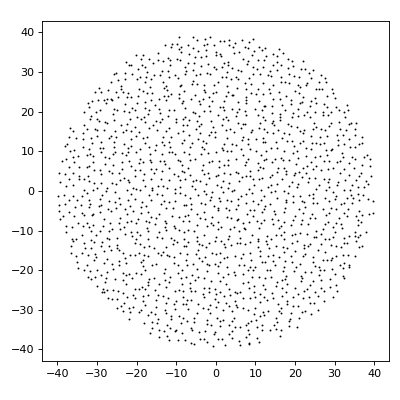
import matplotlib.pyplot as plt

from structure_factor import point_pattern
from structure_factor.point_processes import GinibrePointProcess
from structure_factor.spatial_windows import BallWindow

window = BallWindow(center=[0, 0], radius=40)
point_process = GinibrePointProcess()
point_pattern = point_process.generate_point_pattern(window=window)

ax = point_pattern.plot()
ax.set_aspect("equal", "box")
plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)

code/point_processes/ginibre_pp.py

See also

structure_factor.point_processes.mutual_nearest_neighbor_matching(X, Y, **KDTree_params)[source]

Match the set of points X with a subset of points from Y based on mutual nearest neighbor matching [KLY20]. It is assumed that \(|X| \leq |Y|\) and that each point in X, resp. Y, can have only one nearest neighbor in Y, resp. X.

The matching routine involves successive 1-nearest neighbor sweeps performed by scipy.spatial.KDTree with the euclidean distance.

Parameters

  • X (numpy.ndarray) – Array of size (m, d) collecting points to be matched with a subset of points from Y.

  • Y (numpy.ndarray) – Array of size (n, d) of points satisfying \(m \leq n\).

Keyword Arguments

see (documentation) –

keyword arguments of scipy.spatial.KDTree.

Note

The boxsize keyword argument can be used only when points belong to a box \(\prod_{i=1}^{d} [0, L_i)\) (upper boundary excluded). It allows to consider periodic boundaries, i.e., the toroidal distance is used for searching for nearest neighbors.

Returns

vector of indices matches such that X[i] is matched to Y[matches[i]].

Return type

numpy.ndarray

Example

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.collections import LineCollection

from structure_factor.point_processes import (
    HomogeneousPoissonPointProcess,
    mutual_nearest_neighbor_matching,
)
from structure_factor.spatial_windows import BoxWindow
from structure_factor.utils import meshgrid_to_column_matrix

seed = None
rng = np.random.default_rng(seed)

bounds = np.array([[0, 20], [0, 20]])
window = BoxWindow(bounds)

# Perturbed grid
stepsize = 1.0
ranges = (np.arange(a, b, step=stepsize) for a, b in window.bounds)
X = meshgrid_to_column_matrix(np.meshgrid(*ranges))
shift = rng.uniform(0.0, stepsize, size=window.dimension)
X += shift

# Poisson
rho = (1 + 1) / (stepsize ** window.dimension)
ppp = HomogeneousPoissonPointProcess(rho)
Y = ppp.generate_sample(window, seed=rng)

# Mutual nearest neighbor matching
# To trigger periodic boundary conditions use boxsize
# make sure points belong to Π_i [0, L_i) (upper bound excluded)
boxsize = window.bounds[:, 1]  # default None
matching = mutual_nearest_neighbor_matching(X, Y, boxsize=boxsize)

# Display
fig, ax = plt.subplots(figsize=(10, 10))

ax.scatter(X[:, 0], X[:, 1], s=5, c="blue", label="grid")
ax.scatter(Y[:, 0], Y[:, 1], s=0.4, c="orange", label="Poisson")
ax.scatter(Y[matching, 0], Y[matching, 1], s=5, c="red", label="Poisson matched")
lines = LineCollection(
    [[x, y] for x, y in zip(X, Y[matching])], color="gray", label="matchings"
)
ax.add_collection(lines)

ax.set_aspect("equal", "box")
plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)

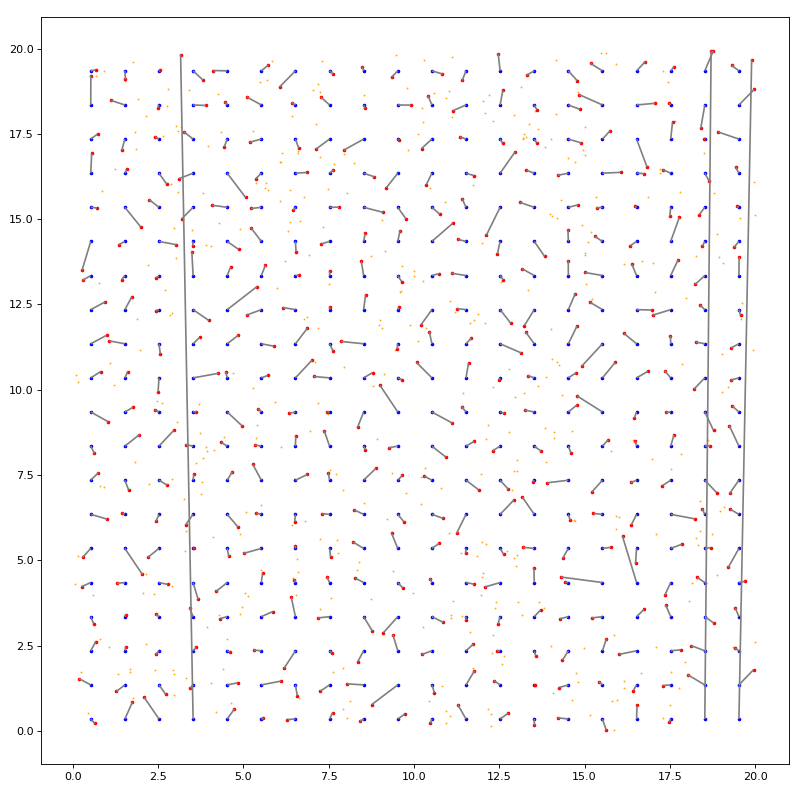
code/point_processes/kly_matching.py

KLY matching