Pair correlation function

Collection of functions used to estimate the pair correlation function of an isotropic point process. The underlying routines call the R package spatstat.

estimate(): Estimates the pair correlation function.
interpolate(): Cleans, interpolates, and extrapolates the results of estimate().
plot(): Plots the results of estimate().

structure_factor.pair_correlation_function.estimate(point_pattern, method='fv', install_spatstat=False, **params)[source]

Estimate the pair correlation function (pcf) of a point process encapsulated in point_pattern (only for stationary isotropic point processes of \(\mathbb{R}^2\)). The available methods are the methods spastat.core.pcf_ppp and spastat.core.pcf_fv of the R package spatstat.

Warning

This function requires the R programming language to be installed on your local machine but, it doesn’t require any knowledge of the programming language R.

Parameters

point_pattern (PointPattern) – Realization of the underlying point process.
method (str, optional) – Trigger the use of the routine pcf.ppp or pcf.fv according to the value "ppp" or "fv". These 2 methods approximate the pair correlation function of a point process from one realization encapsulated in point_pattern. For more details see [BRT15]. Defaults to "fv".
install_spatstat (bool, optional) –
If True, the R package spatstat will be automatically updated or installed (if not present) on your local machine, see also spatstat-interface. Note that this requires the installation of the R programming language.

Keyword Arguments

params (dict) –

if method = "ppp"
- keyword arguments of spastat.explore.pcf.ppp, ex: r, correction …
if method = "fv"
- Kest = dict(keyword arguments of spastat.explore.Kest), ex: rmax …
- fv = dict(keyword arguments of spastat.explore.pcf.fv), ex: method, spar …

Returns

output of spastat.explore.pcf.ppp or spastat.explore.pcf.fv. The first column of the DataFrame is the set of radii on which the pair correlation function was approximated. The others correspond to the approximated pair correlation function with different edge corrections.

Return type

pandas.DataFrame

Example

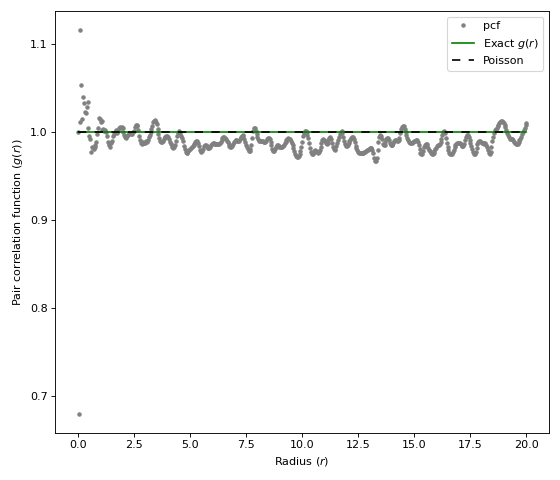
import matplotlib.pyplot as plt

import structure_factor.pair_correlation_function as pcf
from structure_factor.point_processes import HomogeneousPoissonPointProcess
from structure_factor.spatial_windows import BallWindow

point_process = HomogeneousPoissonPointProcess(intensity=1)
window = BallWindow(center=[0, 0], radius=40)
point_pattern = point_process.generate_point_pattern(window=window)

pcf_estimated = pcf.estimate(
    point_pattern, method="fv", Kest=dict(rmax=20), fv=dict(method="c", spar=0.2)
)

pcf.plot(
    pcf_estimated,
    exact_pcf=point_process.pair_correlation_function,
    figsize=(7, 6),
    color=["grey"],
    style=["."],
)
plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)

Definition

The pair correlation function of a stationary isotropic point process \(\mathcal{X}\) of intensity \(\rho\) is the function \(g\) satisfying (when it exists),

\[\mathbb{E} \bigg[ \sum_{\mathbf{x}, \mathbf{y} \in \mathcal{X}}^{\neq} f(\mathbf{x}, \mathbf{y}) \bigg] = \int_{\mathbb{R}^d \times \mathbb{R}^d} f(\mathbf{x}+\mathbf{y}, \mathbf{y})\rho^{2} g(\mathbf{x}) \mathrm{d} \mathbf{x} \mathrm{d}\mathbf{y},\]

for any non-negative smooth function \(f\) with compact support.

For more details, we refer to [HGBLachiezeR22], (Section 2).

See also

PointPattern()
interpolate()
plot()

structure_factor.pair_correlation_function.interpolate(r, pcf_r, clean=True, drop=True, replace=False, nan=0.0, posinf=0.0, neginf=0.0, extrapolate_with_one=True, **params)[source]

Interpolate and then extrapolate the evaluation pcf_r of the pair correlation function (pcf) r.

The interpolation is performed with scipy.interpolate.interp1d.

Parameters

r (numpy.ndarray) – Vector of radii. Typically, the first column of the output of estimate().
pcf_r (numpy.ndarray) – Vector of evaluations of the pair correlation function at r. Typically, a column from the output of estimate().
clean (bool, optional) – If True, a method is chosen to deal with possible outliers (nan, posinf, neginf) of pcf_r. The chosen method depends on the parameters replace and drop. Defaults to True.
drop (bool, optional) – Cleaning method for pcf_r active when it’s set to True simultaneously with clean=True. Drops possible nan, posinf, and neginf from pcf_r with the corresponding values of r.
replace (bool, optional) – Cleaning method for pcf_r active when it’s set to True simultaneously with clean=True. Replaces possible nan, posinf, and neginf values of pcf_r by the values set in the corresponding arguments. Defaults to True.
nan (float, optional) – When replace=True, replacing value of nan present in pcf_r. Defaults to 0.0.
posinf (float, optional) – When replace=True, replacing value of +inf values present in pcf_r. Defaults to 0.0.
neginf (float, optional) – When is replace=True, replacing value of -inf present in pcf_r. Defaults to 0.0.
extrapolate_with_one (bool, optional) –
If True, the discrete approximation vector pcf_r is first interpolated until the maximal value of r, then the extrapolated values are fixed to 1. If False, the extrapolation method of scipy.interpolate.interp1d is used. Note that, the approximation of the structure factor by Ogata quadrature Hankel transform is usually better when set to True. Defaults to True.

Keyword Arguments

params (dict) –

Keyword arguments of the function scipy.interpolate.interp1d.

Returns

Interpolated pair correlation function.

Return type

callable

Example

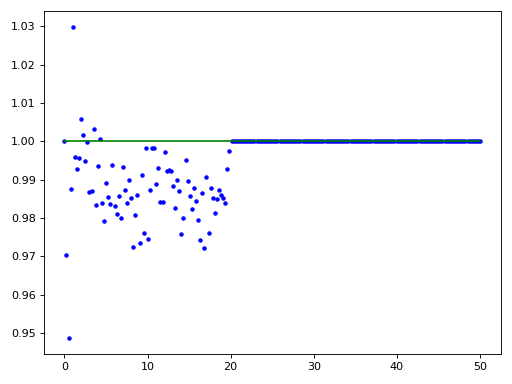
import matplotlib.pyplot as plt
import numpy as np

import structure_factor.pair_correlation_function as pcf
from structure_factor.point_pattern import PointPattern
from structure_factor.point_processes import HomogeneousPoissonPointProcess
from structure_factor.spatial_windows import BallWindow

point_process = HomogeneousPoissonPointProcess(intensity=1)
window = BallWindow(center=[0, 0], radius=40)
point_pattern = point_process.generate_point_pattern(window=window)

pcf_estimated = pcf.estimate(
    point_pattern, method="fv", Kest=dict(rmax=20), fv=dict(method="c", spar=0.2)
)

# Interpolate/extrapolate the results
r = pcf_estimated["r"]
pcf_r = pcf_estimated["pcf"]
pcf_interpolated = pcf.interpolate(
    r=r,
    pcf_r=pcf_r,
    drop=True,
)

x = np.linspace(0, 50, 200)
plt.plot(x, pcf_interpolated(x), "b.")
plt.plot(x, point_process.pair_correlation_function(x), "g")
plt.tight_layout(pad=1)

(Source code, png, hires.png, pdf)